Cooperativismo y Desarrollo, January-April 2020; 8(1), 68-82
Translated from the original in Spanish

Indicador sintético mediante el análisis multivariado de la varianza aplicado al sector turístico

Indicador sintético através da análise multivariada da variância aplicada ao sector do turismo

Reinier Fernández López¹, José Alberto Vilalta Alonso², Arely Quintero Silverio³, Rebeca María Chávez Gomis⁴

¹Universidad de Pinar del Río "Hermanos Saíz Montes de Oca". Facultad de Ciencias Técnicas. Departamento de Matemática. Pinar del Río. Cuba. ORCID: https://orcid.org/0000-0003-1974-9209. Email: rflopez@upr.edu.cu
²Universidad Tecnológica de La Habana (CUJAE). La Habana. Cuba. ORCID: https://orcid.org/0000-0001-7505-8918. Email: jvilalta@ind.cujae.edu.cu
³Universidad de Pinar del Río "Hermanos Saíz Montes de Oca". Facultad de Ciencias Técnicas. Departamento de Matemática. Pinar del Río. Cuba. ORCID: https://orcid.org/0000-0003-2951-8957. Email: arelys@upr.edu.cu
⁴Universidad de Pinar del Río "Hermanos Saíz Montes de Oca". Facultad de Ciencias Técnicas. Departamento de Matemática. Pinar del Río. Cuba. ORCID: https://orcid.org/0000-0001-6854-7596. Email: rebeca.chavez@upr.edu.cu

Received: July 9^th, 2019.
Accepted: January 10^th, 2020.

ABSTRACT

At present, the process of measuring tourist indicators in Pinar del Río does not provide a composite indicator that offers a value as a measure of aggregation of the behavior of tourism indicators, since no procedure that considers several aspects simultaneously is used to obtain it; This causes the decision-making process to be affected. In this sense, the present work consists in developing a composite indicator for the different hotel chains through the use of Multivariate Analysis of Variance techniques, which allows obtaining a global measure to establish a ranking that supports the decision-making process in the different hotel chains in Pinar del Río. Statistical-mathematical methods were used, among others, in order to construct composite indicators.

Keywords: bootstrap; composite indicator; MANOVA; tourism

RESUMEN

En la actualidad, el proceso de medición de indicadores turísticos de Pinar del Río no proporciona un indicador sintético que ofrezca un valor como medida de agregación del comportamiento de los indicadores de turismo, al no emplearse en su obtención procedimientos que consideren varios aspectos simultáneamente; lo anterior provoca que el proceso de toma de decisiones se vea afectado. En este sentido, el presente trabajo consiste en elaborar un indicador sintético para las distintas cadenas hoteleras mediante el empleo de técnicas de Análisis Multivariante de la Varianza, que permita la obtención de una medida global para establecer un ranking que sustente el proceso de toma de decisiones en las distintas cadenas hoteleras de Pinar del Río. Se utilizó, entre otros, los métodos estadístico-matemáticos, con el fin de construir los indicadores sintéticos.

Palabras clave: bootstrap; indicador sintético; MANOVA; turismo

RESUMO

Atualmente, o processo de medição de indicadores turísticos em Pinar del Río não fornece um indicador sintético que ofereça um valor como medida agregadora do comportamento dos indicadores turísticos, uma vez que procedimentos que consideram vários aspectos simultaneamente não são utilizados para os obter; isto faz com que o processo de tomada de decisão seja afetado. Neste sentido, o presente trabalho consiste na elaboração de um indicador sintético para as diferentes cadeias hoteleiras através do uso de técnicas de Análise de Variância Multivariada, que permite obter uma medida global para estabelecer um ranking que suporte o processo de tomada de decisão nas diferentes cadeias hoteleiras de Pinar del Río. Foram utilizados métodos matemáticos-estatísticos, entre outros, a fim de construir os indicadores sintéticos.

Palavras-chave: bootstrap; indicador sintético; MANOVA; turismo

INTRODUCTION

Multivariate analysis is a discipline that is difficult to define, although it generally brings together various statistical techniques which, although many of them were devised by authors who can be called classics, owe their rise and implementation to the dissemination of statistical software and the growing demand for them required by the development of other disciplines (Montanero Fernández, 2008).

That is why research has increasingly used the analysis of variance with several dependent variables as a multivariate analysis technique in recent years. A typical approach has been to perform the analysis of univariate variance for each of the dependent variables. However, this presents the difficulty of type I error inflation (Camacho Rosales, 1990). The multivariate analysis of variance (MANOVA) solves this situation and has global significance techniques (Wilks' Lambda, Hotteling-Lawley's Trace, and Roy's Maximum Root).

MANOVA is a generalization of the analysis of univariate variance for the case of more than one dependent variable (Ramos Alvarez, 2017). The aim is to contrast the significance of one or more factors (independent variables) for the set of dependent variables. It is a statistical method for simultaneously exploring the relationship among several categorical variables and two or more measurable or metric dependent variables (Salgado Horta, 2006).

In the present work, the objective was set: to elaborate a composite indicator, through the use of Multivariate Variance Analysis techniques for the different hotel chains in Pinar del Río.

The application of the MANOVA procedure becomes difficult if a suitable statistical program is not available. For this reason, the statistical language R 3.5.3 and the software R Studio 1.1.463 are used in this research as support for data processing.

MATERIALS AND METHODS

Empirical research methods were used, based on scientific observation and documentary analysis, which allowed characterizing the current situation of measuring tourism indicators in Pinar del Río. The interview technique was used to determine the hotel chains that were included in the research and to obtain information about tourism indicators. Among the mathematical statistical methods, multivariate analysis techniques such as MANOVA were used. Bootstrap was also used as a tool, which allowed for transformations in the variables that did not contemplate normality. Software R 3.5.3 and R Studio 1.1.463 were used to process the data.

At the same time, the measurement method was used for the description and analysis of the behavior of the indicators in each of the dimensions.

Theoretical methods were also used to review the development of the current tourism management processes in Pinar del Río, based on the use of indicators. As a logical method, modelling, for the construction of the functions that guarantee the preparation of the new aggregation procedure. Analysis and synthesis operations were used through the study of the aggregation procedures for the construction of synthetic indicators.

Multivariate analysis of variance: MANOVA

Like analysis of variance (ANOVA), analysis of multivariate variance (MANOVA) is designed to assess the importance of group differences. The only substantial difference between the two procedures is that MANOVA can include several dependent variables, while ANOVA can only handle one (Cuadras, 2014).

Often, these dependent variables are just different measures of the same attribute, but this is not always the case. At a minimum, the dependent variables should have some degree of linearity and share a common conceptual meaning; they should make sense as a group of variables. The basic logic behind a MANOVA is essentially the same as in a univariate analysis of variance. The MANOVA also operates with a set of assumptions, as does the ANOVA, which are (Avendaño Prieto et al., 2014):

1. The observations within each sample should be sampled at random and should be independent of each other.
2. Observations of all dependent variables should follow a multivariate normal distribution in each group.
3. The population covariance matrices for the dependent variables in each group should be the same (this assumption is often referred to as the homogeneity of the covariance matrix assumption or the homocedasticity assumption).
4. The relationships between all pairs of dependent variables for each cell in the data matrix should be linear.

Clarifying that randomness must be guaranteed in the design, the random samples must be predetermined by the researcher in advance, before applying any technique.

Starting from the conceptual bases, when the multivariate technique MANOVA is applied, only one hypothesis is contrasted: that the means of the g groups are equal in the p dependent variables, that the g vectors of group means (called centroids) are equal (Ramos Álvarez, 2017).

Bootstrap methodology

The Bootstrap technique, proposed by Efron (1979), is based on repeatedly extracting samples from a set of training data, adjusting the model of interest for each sample. These are non-parametric methods, which do not require any assumptions about population distribution (Gil Martínez, 2018).

The basic idea is that, if a random sample is taken x=(x₁, x₂, x₃,…, x_n) then the sample can be used to obtain more samples. The procedure is a random resampling (with replacement) of the original sample such that each x_i point has an equal and independent chance of being selected as an element of the new bootstrap sample, that is, P(x^*= x_i) = 1/n, i = 1,2,3,…, n of a distribution with a distribution function F(x). The whole process is an independent repetition of sampling, until a large number of bootstrapped samples are obtained. Multiple statistics can be calculated for each bootstrap sample and, therefore, their distributions can be estimated (Ramirez et al., 2013).

The empirical distribution function F(x)_n, is an estimator of F(x). It can be proved that F(x)_n is a sufficient statistic of F(x); that is, all the information about F(x) contained in the sample is also contained in F(x)_n. Furthermore, F(x)_n is itself the distribution function of a random variable, namely the random variable that is uniformly distributed in the set x=(x₁, x₂, x₃,…, x_n), therefore, the empirical distribution function F(x)_n, is the distribution function of X^* (Gil Abreu, 2014).

It is known that the sum of n random variables, with uniform distribution, quickly approaches the normal distribution (Solanas & Sierra, 1992). Therefore, in the absence of normality, we can use a bootstrap algorithm to obtain B estimates of the mean, based on B samples obtained by resampling over the original sample (Vallejo et al., 2010).

The bootstrap technique, in this research, is applied to estimate means, homogenize variance and achieve the assumption of multivariate normality, treating the sample as a kind of statistical universe. In this study, the algorithm proposed by Efron (1979) was implemented:

1. Given the sample size n, estimate 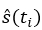, where 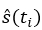in this case, is the mean to be estimated.
2. Generate B bootstrap samples of size n by sampling with replacement of the original sample, assigning each time a probability P(x^*= x_i) = 1/n, i = 1,2,3,…, n and calculate the corresponding values: 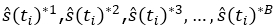, for each of the B bootstrap samples.
3. Estimate the standard error of the estimated parameter 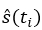, by calculating the standard deviation of the B bootstrap replicates. Thus, we obtain that the standard error is given by:

Where 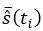corresponds to the average of the estimate of the reliability function evaluated at each time t_i of the bootstrap sample; the procedure is performed based on the first quartile time of interest (Ramírez Montoya et al., 2016).

RESULTS AND DISCUSSION

The application of semi-structured interviews with the actors of the Ministry of Tourism, in Pinar del Río (Mintur) determined the hotel chains or entities to be taken into consideration in this research. The chains selected to establish the synthetic indicators were Cubanacán Hotel Chain, Islazul Hotel Chain and Campismo Popular. From these entities, two indicators were taken, one referring to efficiency: the cost per peso (cost/income) and the other referring to effectiveness: income per tourist (income/quantity of tourists). These indicators allowed the diagnosis of the studied entities, applying the MANOVA tool. The data taken includes the values between January 2006 and December 2018.

From the analysis of the data through the cash flow graphs (Fig. 1), we can see the existence of differences between the entities, with Campismo Popular being the least efficient, but the most effective, while Cubanacán maintains low values of cost per peso and income from tourists. Islazul shows similar cost per peso values as Cubanacán, although it exceeds it in income/tourist, showing good management in terms of efficiency and effectiveness.

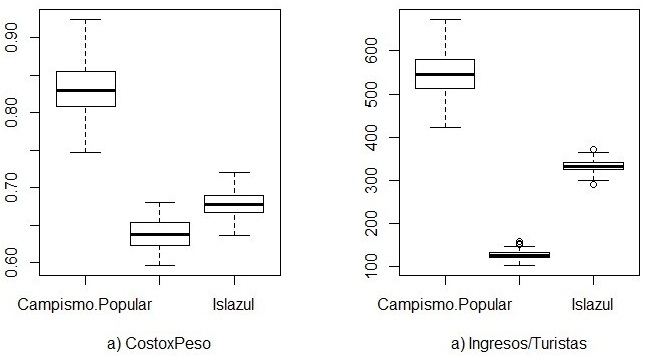
Fig. 1 - Box graphs for cost per peso and average income per tourist for each tourist entity
Source: R, version 3.5.3

Pearson's correlation coefficients between the dependent variables (cost per peso and income per tourist), analyzed in the institution of Campismo and the Cubanacán and Islazul Hotel Chains were -0.20436, -0.13801 and -0.29271 respectively, showing no significant linear relationship between these variables (significance test with value p>0.05). This result, however, is contrary to what would be expected as a result of good tourism management. In figure 2, the above-mentioned can be seen.

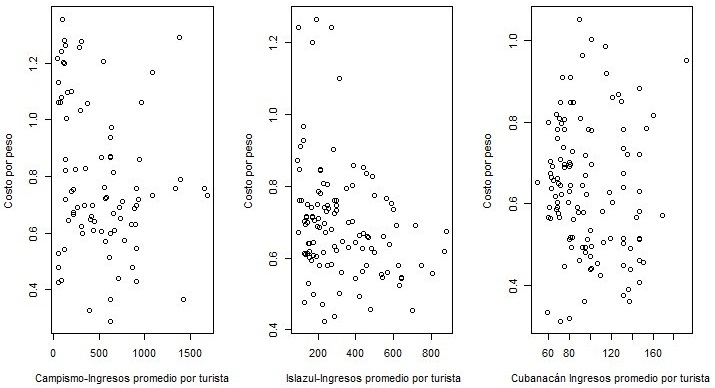
Fig. 2 - Graphs of dispersion cost per peso against average income per tourist for each tourist entity
Source: R, version 3.5.3

When a significance test is performed for correlations between dependent variables, it results in a probability value equal to 0.026 for the total data, rejecting the non-correlation hypothesis.

Figure 3 shows the graphs of dispersion with ellipses, by type of entity, which provides information about the existence of problems with the assumption of constant covariance matrices within the group (Fox et al., 2013).

The ellipses formed by the data of each entity contain notable differences in form, due to the non-compliance with the assumption of equality of variances. This is usually due to the absence of normality.

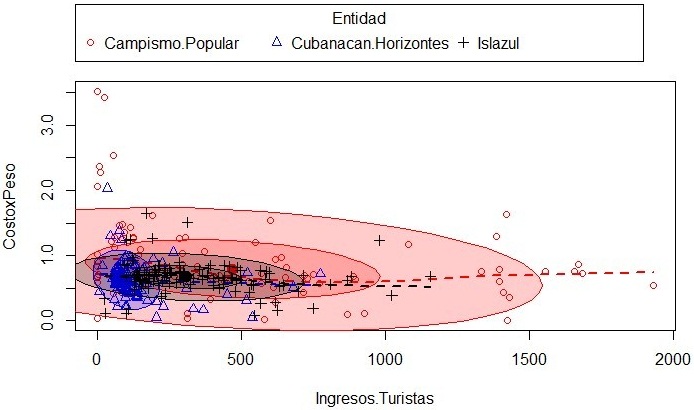
Fig. 3 - Graphs of dispersion with ellipses per tourism entity
Source: R, version 3.5.3

Without the use of hypothesis tests concerning the normality of the data, it can be seen in figure 4 that this assumption is violated. As shown in the figure itself, the set of dependent variables does not maintain normality; by definition of invariant normality, the multivariate normality of the set of dependent variables will not be maintained, and therefore the MANOVA model would lose validity (Ordaz Sanz et al., 2011).

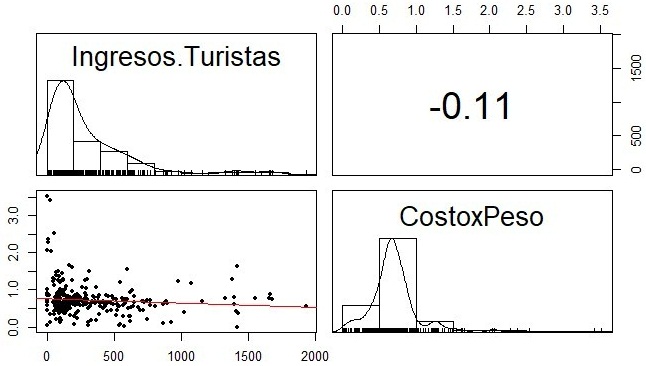
Fig. 4 - Graphs of dispersion with histogram and with correlation coefficient
Source: R, version 3.5.3

Checking the suspicions of the absence of multivariate normality, the multiple normality tests proposed by Mardia (1970) are performed. These tests are determined by R, giving probability values, lower than the significance level (p<0.05), rejecting the null hypothesis (multivariate normality). At this point, it becomes necessary to find an acceptable transformation as an answer to this problem. There is a method that allows to obtain, in a fast way, a transformation that provides certain benefits.

Bootstrap, which is based on the idea of treating the sample as a kind of "statistical universe", sampling repeatedly and using the samples to estimate means, variances, biases and confidence intervals for the parameters of interest (Ramirez Montoya et al., 2016).

The application of the Bootstrap technique allowed the assumption of data normality to be met. Next, a more appropriate MANOVA is carried out, with the aim of checking whether there are differences in the behaviour of the efficiency and effectiveness indicators in the different tourism entities. R facilitated the application of the MANOVA with their respective significance tests (Pillai, Wilks, Hotelling and Roy). According to these significance tests (p<0.05), it can be concluded that there are differences in the parameters: efficiency and effectiveness between the different entities.

Now we proceed to analyze each dependent variable separately, that is, to perform an analysis of the variance of a factor to verify in which dependent variable or variables there are differences between the different entities.

In the output of R, for the analysis of costs by peso, the existence of significant differences between the entities was verified (p<0.05), with an adjusted coefficient of determination of 0.9856, which can be translated as the percentage of variability that is explained by the factors.

Proceeding to analyze the test residues shown in figure 5, it is possible to verify that the basic assumptions are fulfilled, except for the assumption of equality of variance (Residual vs. Fitted values). This is due to the influence in terms of variability that the entity Campismo.

Fig. 5 - Residue Graphs for ANOVA of cost by peso
Source: R, version 3.5.3

Also, in R output, it is verified that the probability value is lower than the significance level, which is interpreted as the existence of statistically significant differences between these entities, regarding the behavior of the dependent variable income from tourists, with an adjusted coefficient of determination of 0.9094.

Analyzing the residues of the model (Fig. 6), it can be seen that there is no homogeneity of variances (Residual vs. Fitted values), which is due to the differences imposed by Campismo Popular in terms of its own characteristics, with respect to the rest of the other entities.

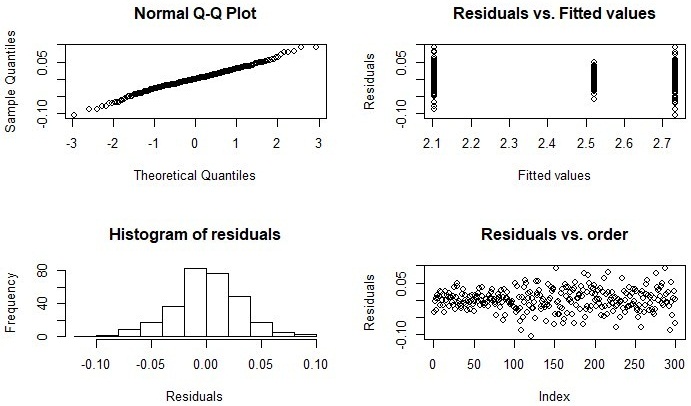
Fig. 6 - Residue graphs for ANOVA of average incomes per tourist
Source: R, version 3.5.3

By repeating the procedure for the analysis of variance, but without including Campismo Popular, the assumption of homogeneity of variances for the entities Islazul and Cubanacán is achieved, thus corroborating what was explained above. From here, cleaner results can be obtained by applying the tool of multivariate data analysis. Figure 7 shows the fulfillment of this assumption.

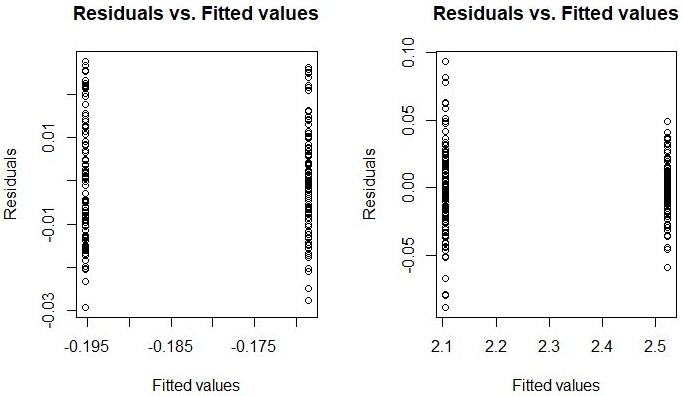
Fig. 7 - Residue graphs to do the analysis of the equal variance assumption
Source: R, version 3.5.3

When carrying out the ANOVA, without including the entity of Campismo Popular, the results shown by the software for the variables cost per peso and income per tourist, show significant differences among the entities involved for both indicators (p<0.01), with determination coefficients of 0.53 and 0.985 respectively.

For the conformation of the composite indicator (Table 1), it was necessary to assign to each sub-indicator the same weight as the others; in this case, the determination coefficients R² adding the information by means of a sum (Torres Delgado & López Palomeque, 2017). The weighting and aggregation are usually done in successive levels, so that previously a series of variables are weighted and aggregated to construct the sub-indicators related to a certain dimension and, subsequently, these are added to construct the synthetic indicator (Nardo et al., 2005). Thus, the indicator for a unit i is defined as 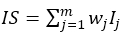where w_j is the weight assigned to the indicator j.

Table 1 - Formulation of efficiency and effectiveness indicators

Entity	Cost by peso R2	Income per tourist R2	Cost by peso 1-CV	Income per tourist 1-CV	Weighted sum	Ranking
Cubanacán	0.5313	0.985	0.6012	0.0794	0.3976	2
Campismo	0.9856	0.9094	0.3353	0.0208	0.3493	3
Islazul	0.5313	0.985	0.6676	0.3734	0.7224	1

Source: Own elaboration

As a standardized indicator, the complement of the coefficient of variation (CV) was used, which measures the degree of homogeneity of the values of the variable. The CV is a measure of the degree of heterogeneity; it is used primarily to compare periods or stages and allows comparisons to be made between heterogeneous data sets.

Once the weights w_j and the standardized indicator have been determined, the values of the composite indicator are obtained by means of a weighted sum of the standardized values of the system's indicators (Parada et al., 2015).

In table 1, it can be seen that the hotel chain with the best results is Islazul, while Campismo Popular shows a less adequate situation in terms of efficiency and effectiveness, which is more distant, in terms of scores, from the rest of the entities, above all due to the problems of efficiency that it presents.

This paper demonstrates the importance of multivariate analysis of variance in the diagnosis of the efficiency and effectiveness of tourism activity, based on the calculation of a composite index.

Its application in the province of Pinar del Río, Cuba, made it possible to determine the scores to build a ranking among the tourism entities, becoming a tool for the strategic analysis of the sector.

REFERENCES

Avendaño Prieto, B. L., Avendaño Prieto, G., Cruz, W., & Cárdenas Avendaño, A. (2014). Guía de referencia para investigadores no expertos en el uso de estadística multivariada. Diversitas: Perspectivas en Psicología, 10(1), 13-27. http://www.scielo.org.co/scielo.php?script=sci_abstract&pid=S1794-99982014000100002

Camacho Rosales, J. (1990). Interpretación del MANOVA: Análisis de la importancia de las variables dependientes. Investigaciones, 10.

Cuadras, C. M. (2014). Nuevos métodos de análisis multivariante. CMC Editions.

Efron, B. (1979). Bootstrap methods: Another look at jackknife. The Annals of Statistics, 7(1), 1-26. https://projecteuclid.org/download/pdf_1/euclid.aos/1176344552

Fox, J., Friendly, M., & Weisberg, S. (2013). Hypothesis Tests for Multivariate Linear Models Using the car Package. The R Journal, 5(1), 39-52. https://doi.org/10.32614/RJ-2013-004

Gil Abreu, S. N. (2014). Bootstrap en poblaciones finitas [Máster Oficial en Estadística Aplicada]. Universidad de Granada.

Gil Martínez, C. (2018). Métodos de remuestreo y validación de modelos: Validación cruzada y bootstrap.

Mardia, K. V. (1970). Measures of multivariate skewness and kurtosis with applications. Biometrika, 57(3), 519-530. https://doi.org/10.2307/2334770

Montanero Fernández, J. (2008). Análisis Multivariante. Universidad de Extremadura.

Nardo, M., Saisana, M., Saltelli, A., Tarantola, S., Hoffman, A., & Giovannini, E. (2005). Handbook on Constructing Composite Indicators: Methodology and User Guide. OECD.

Ordaz Sanz, J. A., Melgar Hiraldo, M. del C., & Rubio Castaño, C. M. (2011). Métodos estadísticos y econométricos en la empresa y para finanzas. Universidad Pablo de Olavide. https://www.upo.es/export/portal/com/bin/portal/upo/profesores/jaordsan/profesor/1381243330001_metodos_estadisticos_y_econometricos_en_la_empresa_y_para_finanzas.pdf

Parada, S., Fiallo, J., & Blasco Blasco, O. (2015). Construcción de indicadores sintéticos basados en juicio experto: Aplicación a una medida integral de la excelencia académica. Revista Electrónica de Comunicaciones y Trabajos de ASEPUMA, 16(1), 51-67. https://dialnet.unirioja.es/servlet/articulo?codigo=5601445

Ramírez, I. C., Barrera, C. J., & Correa, J. C. (2013). Efecto del tamaño de muestra y el número de réplicas bootstrap. Ingeniería y Competitividad, 15(1), 93-101.

Ramírez Montoya, J., Osuna Vergara, I., Rojas Mora, J., & Guerrero Gómez, S. (2016). Remuestreo Bootstrap y Jackknife en confiabilidad: Caso Exponencial y Weibull. Revista Facultad de Ingeniería, 25(41), 55-62. http://www.scielo.org.co/scielo.php?script=sci_arttext&pid=S0121-11292016000100006

Ramos Álvarez, M. M. (2017). Curso de análisis de investigaciones con programas informáticos. Universidad de Jaén.

Salgado Horta, D. (2006). Métodos estadísticos multivariados.

Solanas, A., & Sierra, V. (1992). Bootstrap: Fundamentos e introducción a sus aplicaciones. Anuario de Psicología, 55, 143-154.

Torres Delgado, A., & López Palomeque, F. (2017). The ISOST index: A tool for studying sustainable tourism. Journal of Destination Marketing & Management, 8, 281-289. https://doi.org/10.1016/j.jdmm.2017.05.005

Vallejo, G., Fernández, M. P., Tuero, E., & Livacic Rojas, P. E. (2010). Análisis de medidas repetidas usando métodos de remuestreo. Anales de Psicología, 26(2), 400-409. http://www.redalyc.org/articulo.oa?id=16713079025

Conflict of interest:

Authors declare not to have any conflict of interest.

Authors' contribution:

The authors have participated in the writing of the paper and the analysis of the documents.